En este nuevo artículo de Aprende Machine Learning explicaremos qué son los outliers y porqué son tan importantes, veremos un ejemplo práctico paso a paso en Python, visualizaciones en 1, 2 y 3 dimensiones y el uso de una librería de propósito general.
Puedes encontrar la Jupyter Notebook completa en GitHub.

¿Qué son los Outliers?
Es interesante ver las traducciones de “outlier” -según su contexto- en inglés:
- Atípico
- Destacado
- Excepcional
- Anormal
- Valor Extremo, Valor anómalo, valor aberrante!!
Eso nos da una idea, ¿no?
Es decir, que los outliers en nuestro dataset serán los valores que se “escapan al rango en donde se concentran la mayoría de muestras”. Según Wikipedia son las muestras que están distantes de otras observaciones.
Detección de Outliers
¿Y por qué nos interesa detectar esos Outliers? Por que pueden afectar considerablemente a los resultados que pueda obtener un modelo de Machine Learning… Para mal… ó para bien! Por eso hay que detectarlos, y tenerlos en cuenta. Por ejemplo en Regresión Lineal ó algoritmos de Ensamble puede tener un impacto negativo en sus predicciones.
Outliers Buenos vs Outliers Malos
Los Outliers pueden significar varias cosas:
- ERROR: Si tenemos un grupo de “edades de personas” y tenemos una persona con 160 años, seguramente sea un error de carga de datos. En este caso, la detección de outliers nos ayuda a detectar errores.
- LIMITES: En otros casos, podemos tener valores que se escapan del “grupo medio”, pero queremos mantener el dato modificado, para que no perjudique al aprendizaje del modelo de ML.
- Punto de Interés: puede que sean los casos “anómalos” los que queremos detectar y que sean nuestro objetivo (y no nuestro enemigo!)
Instala tu ambiente de desarrollo python con Anaconda, aquí explicamos cómo
Muchas veces es sencillo identificar los outliers en gráficas. Veamos ejemplos de Outliers en 1, 2 y 3 dimensiones.
Outliers en 1 dimensión
Si analizáramos una sola variable, por ejemplo “edad”, veremos donde se concentran la mayoría de muestras y los posibles valores “extremos”. Pasemos a un ejemplo en Python!
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
import matplotlib.pyplot as plt import numpy as np edades = np.array([22,22,23,23,23,23,26,27,27,28,30,30,30,30,31,32,33,34,80]) edad_unique, counts = np.unique(edades, return_counts=True) sizes = counts*100 colors = ['blue']*len(edad_unique) colors[-1] = 'red' plt.axhline(1, color='k', linestyle='--') plt.scatter(edad_unique, np.ones(len(edad_unique)), s=sizes, color=colors) plt.yticks([]) plt.show() |
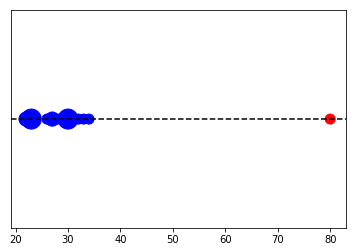
En el código, importamos librerías, creamos un array de edades con Numpy y luego contabilizamos las ocurrencias.
Al graficar vemos donde se concentran la mayoría de edades, entre 20 y 35 años. Y una muestra aislada con valor 80.
Outliers en 2 Dimensiones
Ahora supongamos que tenemos 2 variables: edad e ingresos. Hagamos una gráfica en 2D. Además, usaremos una fórmula para trazar un círculo que delimitará los valores outliers: Los valores que superen el valor de la “media más 2 desvíos estándar” (el área del círculo) quedarán en rojo.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
from math import pi salario_anual_miles = np.array([16,20,15,21,19,17,33,22,31,32,56,30,22,31,30,16,2,22,23]) media = (salario_anual_miles).mean() std_x = (salario_anual_miles).std()*2 media_y = (edades).mean() std_y = (edades).std()*2 colors = ['blue']*len(salario_anual_miles) for index, x in enumerate(salario_anual_miles): if abs(x-media) > std_x: colors[index] = 'red' for index, x in enumerate(edades): if abs(x-media_y) > std_y: colors[index] = 'red' plt.scatter(edades, salario_anual_miles, s=100, color=colors) plt.axhline(media, color='k', linestyle='--') plt.axvline(media_y, color='k', linestyle='--') v=media #y-position of the center u=media_y #x-position of the center b=std_x #radius on the y-axis a=std_y #radius on the x-axis t = np.linspace(0, 2*pi, 100) plt.plot( u+a*np.cos(t) , v+b*np.sin(t) ) plt.xlabel('Edad') plt.ylabel('Salario Anual (miles)') plt.show() |
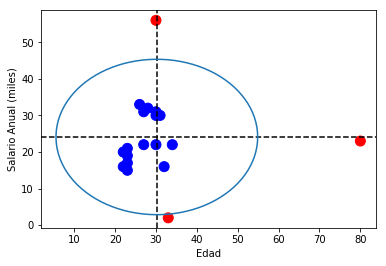
Veamos -con la ayuda de seaborn-, la línea de tendencia de la misma distribución con y sin outliers:
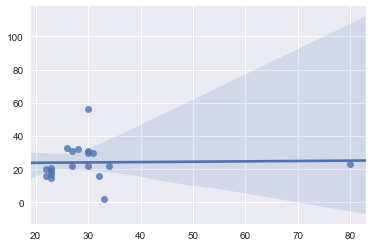
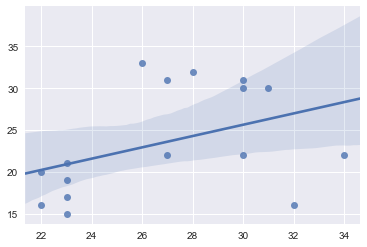
Con esto nos podemos dar una idea de qué distinto podría resultar entrenar un modelo de Machine Learning con ó sin esas muestras anormales.
Visualizar Outliers en 3D
Vamos viendo que algunas de las muestras del dataset inicial van quedando fuera!
¿Qué pasa si añadimos una 3ra dimensión nuestro dataset? Por ejemplo, la dimensión de “compras por mes” de cada usuario.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
from mpl_toolkits.mplot3d import Axes3D fig = plt.figure(figsize=(7,7)) ax = fig.gca(projection='3d') compras_mes = np.array([1,2,1,20,1,0,3,2,3,0,5,3,2,1,0,1,2,2,2]) media_z = (compras_mes).mean() std_z = (compras_mes).std()*2 for index, x in enumerate(compras_mes): if abs(x-media_z) > std_z: colors[index] = 'red' ax.scatter(edades, salario_anual_miles, compras_mes, s=20, c=colors) plt.xlabel('Edad') plt.ylabel('Salario Anual (miles)') ax.set_zlabel('Compras mensuales') plt.show() |
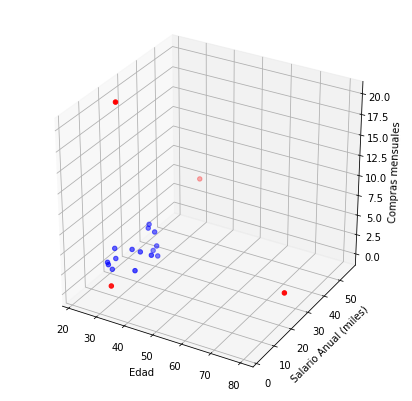
En el caso de las compras mensuales, vemos que aparece un nuevo “punto rojo” en el eje Z. Debemos pensar si es un usuario que queremos descartar ó que por el contrario, nos interesa analizar.
Outliers en N-dimensiones
La realidad es que en los modelos con los que trabajamos constan de muchas dimensiones, podemos tener 30, 100 ó miles. Entonces ya no parece tan sencillo visualizar los outliers.
Podemos seguir detectando los outliers “a ciegas” y manejarlos. O mediante una librería (más adelante se comenta en el artículo).
Podemos graficar múltiples dimensiones haciendo una reducción de dimensiones con PCA ó con T-SNE.
NOTA: tenemos que pensar que -suponiendo que no hay error en los datos- un valor que analizado en 1 sóla dimensión es un Outlier, analizado en conjunto en “N-dimensiones” puede que NO LO SEA. Entonces no siempre es válida la estrategia de analizar la variable aislada del resto.
Imaginemos que luego de aplicar PCA sobre un conjunto obtenemos los siguientes clusters:

Aquí vemos claramente que hay valores que no “encajan” en ningún conjunto: los outliers. Esto a veces se podría corresponder con “Anomaly detection”.
Una gráfica de detección sencilla: Boxplots
Una gráfica bastante interesante de conocer es la de los Boxplots, muy utilizados en el mundo financiero. En nuestro caso, podemos visualizar las variables y en esa “cajita” veremos donde se concentra el 50 por ciento de nuestra distribución (percentiles 25 a 75), los valores mínimos y máximos (las rayas en “T”) y -por supuesto- los outliers, esos “valores extraños” y alejados.
|
1 2 3 4 |
green_diamond = dict(markerfacecolor='g', marker='D') fig, ax = plt.subplots() ax.set_title('Boxplot por Edades') ax.boxplot(edades, flierprops=green_diamond, labels=["Edad"]) |
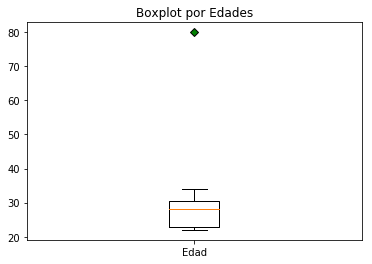
Una vez detectados, ¿qué hago?
Según la lógica de negocio podemos actuar de una manera u otra.
Por ejemplo podríamos decidir:
- Las edades fuera de la distribución normal, eliminar.
- El salario que sobrepasa el límite, asignar el valor máximo (media + 2 sigmas).
- Las compras mensuales, mantener sin cambios.
PyOD: Librería Python para Detección de Outliers
En el código utilicé una medida conocida para la detección de outliers que puede servir: la media de la distribución más 2 sigmas como frontera. Pero existen otras estrategias para delimitar outliers.
Una librería muy recomendada es PyOD. Posee diversas estrategias para detectar Outliers. Ofrece distintos algoritmos, entre ellos Knn que tiene mucho sentido, pues analiza la cercanía entre muestras, PCA, Redes Neuronales, veamos cómo utilizarla en nuestro ejemplo.
|
1 2 3 4 5 6 7 8 9 10 11 |
!pip install pyod # instala la librería from pyod.models.knn import KNN import pandas as pd X = pd.DataFrame(data={'edad':edades,'salario':salario_anual_miles, 'compras':compras_mes}) clf = KNN(contamination=0.18) clf.fit(X) y_pred = clf.predict(X) X[y_pred == 1] |
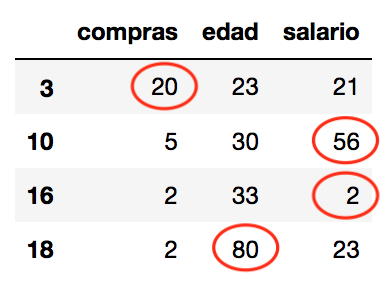
Para problemas en la vida real, con múltiples dimensiones conviene apoyarnos en una librería como esta que nos facilitará la tarea de detección y limpieza/transformación del dataset.
Conclusiones
Hemos visto lo importante que son los outliers y el impacto que pueden tener al entrenar un modelo de ML. La mayoría de los datasets tendrán muestras “fuera de rango”, por lo que debemos tenerlas en cuenta y decidir cómo tratarlas.
Para algunos problemas, nos interesa detectar esos outliers y de hecho será nuestro objetivo localizar esas anomalías.
Para trabajar con muestras con decenas o cientos de dimensiones nos conviene utilizar una librería como PyOd que realiza muy bien su trabajo!
Espero que el artículo haya sido de tu interés! No olvides compartir y para cualquier consulta deja tu comentario!
Suscripción al Blog
Recibe los próximos artículos sobre Machine Learning, estrategias, teoría y código Python en tu casilla de correo!
NOTA: algunos usuarios reportaron que el email de confirmación y/o posteriores a la suscripción entraron en su carpeta de SPAM. Te sugiero que revises y recomiendo que agregues nuestro remitente a tus contactos para evitar problemas. Gracias!
Recursos
Descarga la Notebook Ejercicio_Outliers que acompaña este artículo desde mi cuenta de Github
Enlaces de Interés
La libreria pyod anomaly detection
How to Identify Outliers in your Data
Effective Outlier Detection Techniques in Machine Learning
How to Make Your Machine Learning Models Robust to Outliers
Three methods to deal with outliers
Outlier Detection and Anomaly Detection with Machine Learning
El libro del Blog
Si te gustan los contenidos del blog y quieres darme una mano, puedes comprar el libro en papel, ó en digital.

Hola, el post me parece sencillamente genial para quienes, como yo, estamos empezando a caminar en este mundo. Felicidades.
Tengo una pregunta de inexperto:
Hasta donde conozco kNN es un algoritmo de clasificación de aprendizaje supervisado, y en tu código de ejemplo haces esto:
clf.fit(X)
Mi pregunta es: ¿dónde le pasas los valores target al entrenarlo
Gracias y un saludo